插值
重心坐标

已知三角形三个顶点的坐标,那么三角形所在平面的任意一点都看看有用以下公式来表示:
\((x,y)=\alpha A+\beta B+\gamma C\)
且满足\(\alpha +\beta +\gamma=1\)
如果这个点在三角形内部,那么\(\alpha\)、\(\beta\)和\(\gamma\)都是正数。
由\(\alpha\)、\(\beta\)和\(\gamma\)就是重心坐标:\((\alpha,\beta\gamma)\)
给出三角形内一点,可以根据三角形的面积求出它的重心坐标:
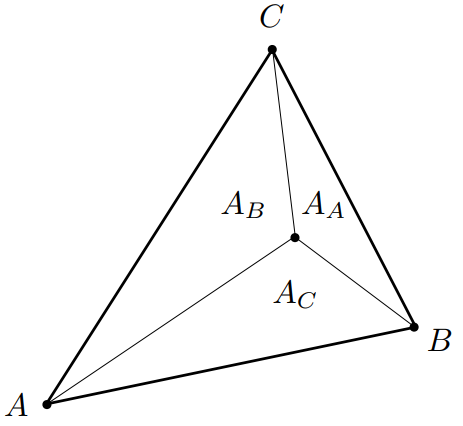
\(\alpha =\frac{A_A}{A_A+A_B+A_C}\)
\(\beta =\frac{A_B}{A_A+A_B+A_C}\)
\(\gamma =\frac{A_C}{A_A+A_B+A_C}\)
三角形重心的重心坐标:\((\frac{1}{3},\frac{1}{3},\frac{1}{3}\)
重心坐标的简化计算方式:
\(\alpha =\frac{-\left(x-x_B\right)\left(y_C-y_B\right)+\left(y-y_B\right)\left(x_C-x_B\right)}{-\left(x_A-x_B\right)\left(y_C-y_B\right)+\left(y_A-y_B\right)\left(x_C-x_B\right)}\)
\(\beta =\frac{-\left(x-x_C\right)\left(y_A-y_C\right)+\left(y-y_C\right)\left(x_A-x_C\right)}{-\left(x_B-x_C\right)\left(y_A-y_C\right)+\left(y_B-y_C\right)\left(x_A-x_C\right)}\)
\(\gamma =1-\alpha-\beta\)
插值
得到三角形内任意一点的重心坐标后,可以将重心坐标乘上对应顶点的属性,得到三角形内任意一点的属性。
\(V=\alpha V_A+\beta V_B+\gamma V_C\)

\(V_A\),\(V_B\),\(V_C\)可以是位置,纹理坐标,颜色,法线,深度,材质属性…
注意,在投影变换下,重心坐标并不能保证不变,即空间中的三角形重心坐标和投影后的中心坐标很可能不相同。
所以在求投影坐标时,要在空间中求,而不能在进行投影变换后再求
纹理映射
应用纹理
根据三角形顶点坐标插值出每个点的纹理坐标,然后在纹理图上找到对应的点,也就那个点的漫反射系数。
纹理过小
近似查询
纹理上的像素—纹理元素
求出一点的对应的纹理坐标后,会找到距离最近的纹理元素并着色。
但是当模型精度大于纹理精度时,会发生多个像素的纹理元素相同。

找最近的纹理元素时,红色的点会找到纹理样本u11

双线性插值
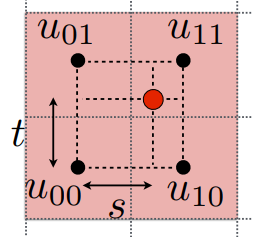
在双线性插值时,会找到红点周围的四个纹理样本。
可以找到红点距离左下角的水平距离\(s\)和竖直距离\(t\)。(认为每两个纹理元素之间的距离为1)
线性插值:\(lerp(x,v_0 ,v_1 )=v_0 +x(v_1 -v_0 )\)
定义一个\(x\),在\(v_0\)到\(v_1\)之间
先用\(s\)在左下角和右下角进行线性插值得到\(u_0\),再在左上角和右上角进行线性插值\(u_1\)
再用\(t\)在\(u_0\)和\(u_1\)之间进行插值,得到红点处的纹理值。
双三次插值
双三次插值(Bicubic):采用周围16个像素进行双三次插值,得到的质量更好。
纹理过大
当纹理过大时,远处的像素点会发生一个像素点代表了一大片的纹理元素

这时就会出现摩尔纹
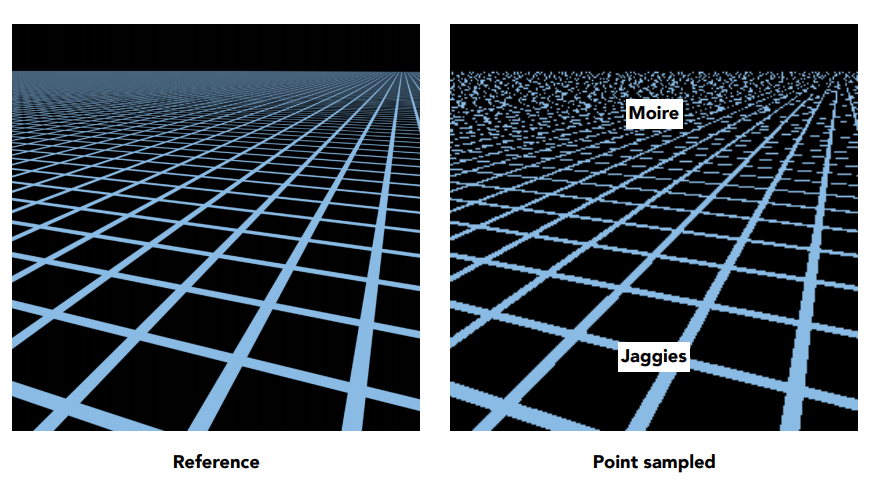
从信号的角度来说,就是采样频率低于信号的变化频率产生了畸变。
利用超采样后:

但是其开销会非常大。
所以现在想要不采样,直接得到平均后的结果。
Mipmap
Mipmap可以做到在不采样的情况下,直接得到平均后的结果。它可以做到快速、近似的正方形范围平均像素查询。
但注意,得到的结果只是近似值,并且只能查询正方形范围。
假设有一张分辨率为128*128的纹理图,将原图称为Level 0。
将原图的长宽都压缩一半,称为Level 1,不断压缩长宽,直到图片变成1*1。

Mipmap占用的空间是原图的\(\frac{4}{3}\),即空间开销增加了\(\frac{1}{3}\)。其实就对平均像素进行预处理,提前得到各层次的平均像素,也就是用空间换时间。
图像金字塔也就是指Mipmap,Mipmap的每一个等级也被称为“层”(D)。
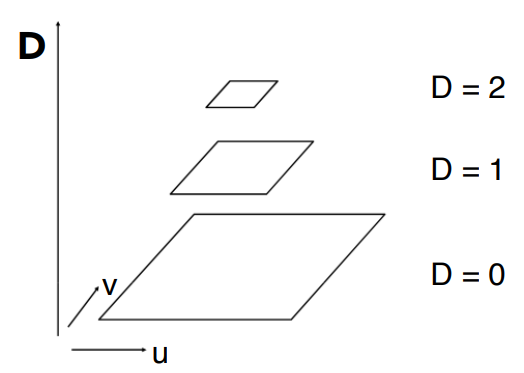
计算Mipmap等级
要计算一个像素的Mipmap等级,可以先找出该像素以及其上方、右方两个像素在纹理图上对应的坐标,然后再根据这三个点的坐标求出采样正方形的边长。
\(L=\max \left(\sqrt{\left(\frac{d u}{d x}\right)^2+\left(\frac{d v}{d x}\right)^2}, \sqrt{\left(\frac{d u}{d y}\right)^2+\left(\frac{d v}{d y}\right)^2}\right)\)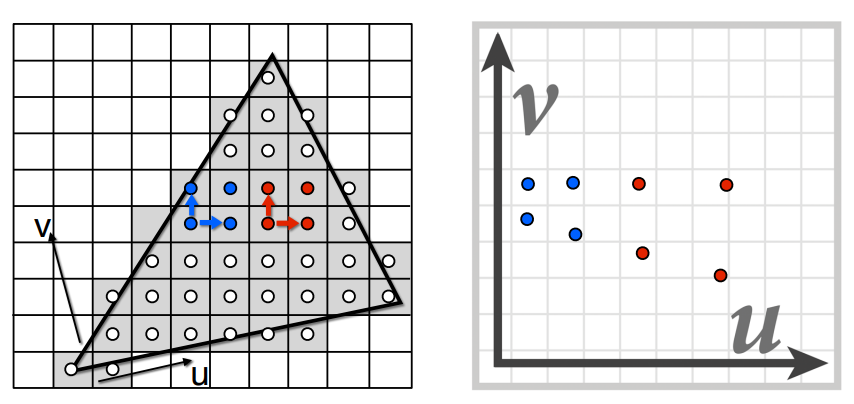

再根据边长L就能求出等级了
\(D=\log _2 L\)
三线性插值
将Mipmap等级可视化后:

可以发现,其等级变化非常的不平滑。其原因就是计算Mipmap时,只对离散的等级进行了采样。
可以利用三线性插值的方法求出连续等级的Mipmap。
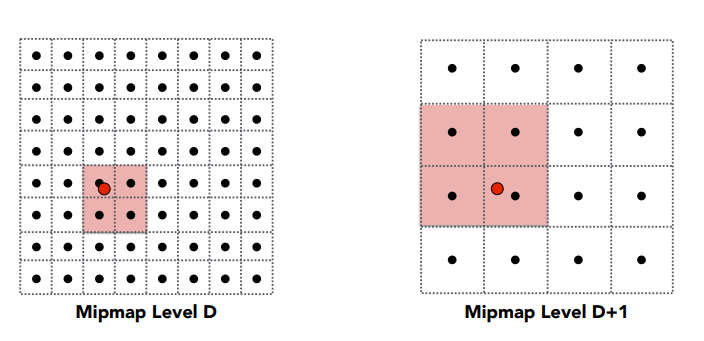
先用双线性插值得到采样点原本所在的等级D的纹理值,再取出采样点高一个等级D+1层的纹理值,再将两个值再进行插值。
这样得到的Mipmap等级就非常平滑

各向异性过滤
但如果采用Mipmap来解决上面的摩尔纹问题,产生的图像是这样的:

远处的细节完全消失了。
其原因就是, 每个像素点在纹理图上对应的范围并不一定是正方形的。
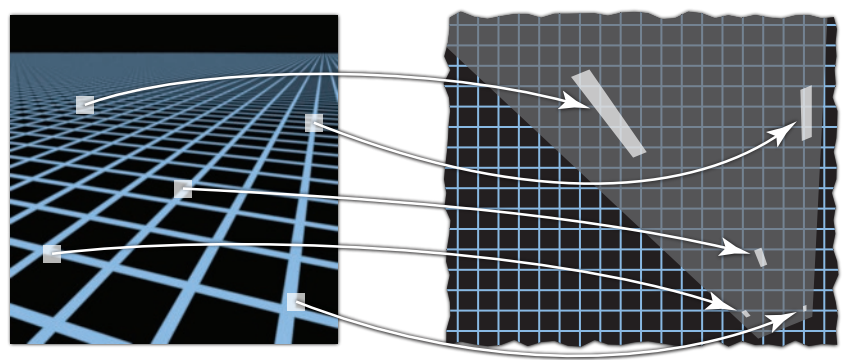
对于矩形的采样区域,全部会被近似成正方形,得到的误差就会变大。
各向异性可以很好的解决矩形区域的采样问题。
Mipmap计算出的是长和宽同时缩小时的图像,而各向异性过滤还会生成长宽不同时压缩时的图像。
下方图像的左上角是原图,从左往右,横向被不断压缩,从上往下,纵向不断压缩。这样各向异性过滤就可以很好的应对矩形采样区域了。Mipmap正好是在这张图的对角线上。

各向异性过滤的总空间开销是原图的3倍,也就是额外开销为原图的2倍。
这时各向异性过滤得到的图像:

但各向异性无法解决采样矩形在纹理图中斜放的情况。
高级纹理映射
纹理不止可以用来表示模型表明的颜色,还可以表示模型的各种性质。
环境光纹理
将环境光提前运算好并作为纹理应用在物体表明,可以减少计算量。

球体纹理
球形纹理
在对一个球应用纹理的时候,球体的纹理会是这样的:

很明显,在球体的两极处会产生严重的畸变
立方体纹理
向量沿着那个方向映射到立方体点。
立方体有6个正方形纹理贴图。
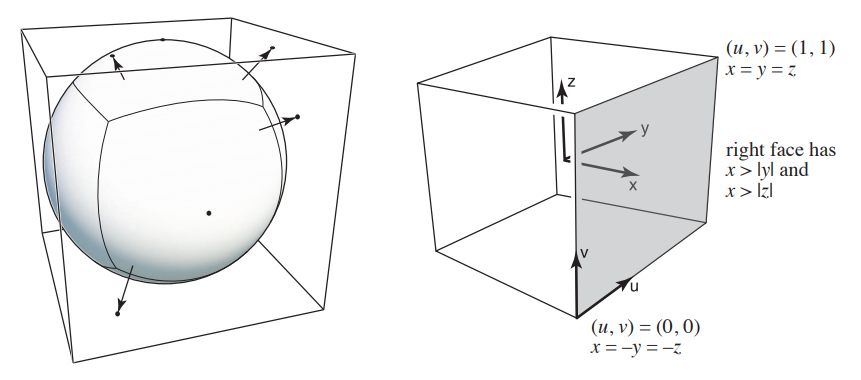
这样可以很好的解决球形纹理带来的畸变问题,但是需要在查询纹理的时候多一步计算:查询纹理的所在的面。

凹凸贴图
利用凹凸贴图可以伪造详细的几何图形。

凹凸贴图可以添加表面细节而不添加更多三角形。
其会修改每个像素的表面法线,并且仅用于着色计算。
由纹理定义的每个纹理元素的“高度偏移”,也就纹理表示每个纹理元素的位置会沿着原法线上移或下移多少,这会改变纹理的法线,从而影响到着色计算。将最终得到的法线称为扰动法线。
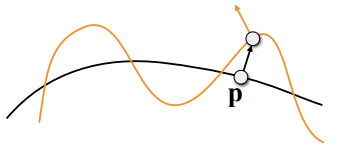
在二维空间中,可以根据以下步骤计算扰动法线:
先假设原法线为\(n(p)=(0,1)\)
根据导数的定义,得出p处的导数为\(dp=c*[h(p+1)-h(p)]\)
将得到的导数看做向量,逆时针旋转90°也就得到了垂直的向量,在进行归一化,得到扰动向量:\(n(p)=(-dp,1).normalized()\)
在三维空间中,计算扰动法线的步骤和在二维空间中类似:
设原法线为\(n(p)=(0,0,1)\)
p处的导数为:
\(\frac{dp}{du}=c1*[h(u+1)-h(u)]\)
\(\frac{dp}{dv}=c2*[h(v+1)-h(v)]\)
同样进行旋转然后归一化得到扰动向量:\(n=(-\frac{dp}{du},-\frac{dp}{dv},1).normalized()\)
注意,这里全部假设原法线为\(n(p)=(0,0,1)\),在实际运算中,会依据原法线,建立一个局部的微坐标系,将相关坐标全部转换到微坐标系中,再运算扰动法线,然后再进行逆运算,得到结果。
位移贴图
位移贴图和凹凸贴图相似,但更为高级。
凹凸贴图只改变了纹理的法向量,但位移贴图会改变模型中三角形顶点的位置。
凹凸贴图无法产生阴影,并且模型整体的阴影在边缘处也没有被改变。
位移贴图会产生阴影,并且模型整体的阴影在边缘处也会被改变。
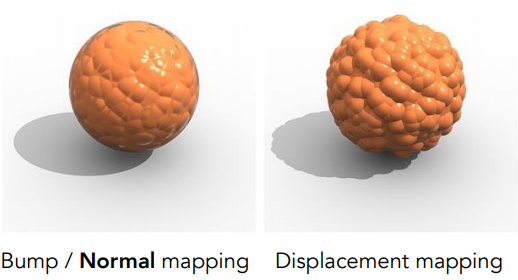
位移贴图要求模型的面极为精细,即信号变化频率要大于位移贴图的频率。






Comments | NOTHING