隐式表示
几何的隐式表示,就是并不直接定义几何体的面,而是用函数来描述,即几何体上的点满足某种特定的关系。
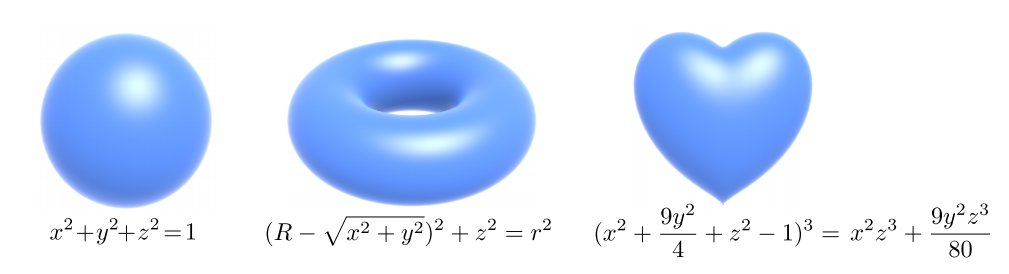
可以很快速的找到某个点是否在几何体表面上或者内部、外部,但是只适用于简单的几何体,对于复杂的几何体,其函数将非常复杂,并且无法从函数直接看出几何体是什么。
显示表示
显示表示主要分为两种:直接给出每个点的坐标,或者通过参数映射。前者很好理解,这里详解参数映射的方式。
先定义一个函数,将\((u,v)\)输入到函数中,就能得到\((x,y,z)\)
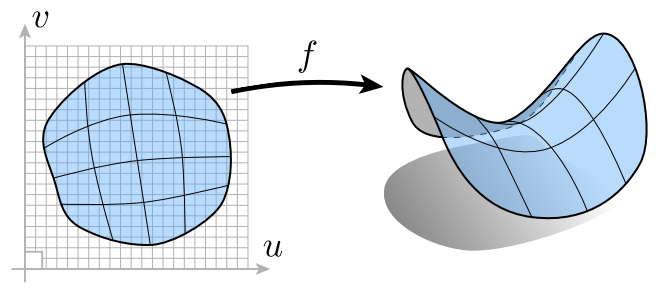
例如,定义一个函数\(f(u,v)=((2+\cos u) \cos v,(2+\cos u)\sin v,\sin u)\)
得到的几何体:

函数\(f(u,v)=(\cos u \cos v,\sin u \sin v,\cos v)\),得到的几何体:

其他的隐式表示
通过布尔运算组合隐式几何
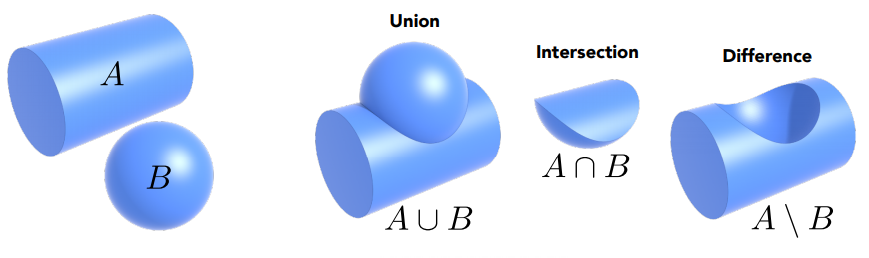
上图分别表示A物体和B物体的加、交、减运算。这种方式在各种建模软件中广泛应用。
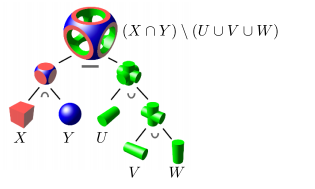
这种运算可以得到复杂的几何体。
距离函数
距离函数表示到达几何体表面的最小距离。

如上图,有A,B两个物体遮挡住了后面的物体,如果只进行简单的合并,会得到左侧完全遮挡,中间为半透明状态,右边未遮挡。
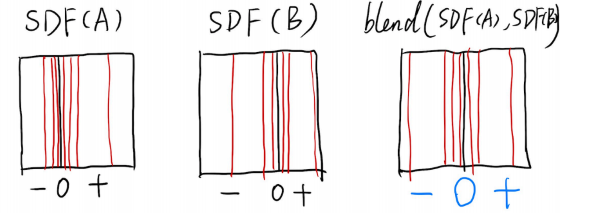
如上图,如果给A,B两物体定义距离函数,即表示某一点到达A,B物体的最小距离,将A,B物体的距离函数相加,会得到一个新的距离函数,令新的距离函数等于0,即找到距离为0的点,并连接成新的平面,就能得到一个在A,B之间的平面。
下图表示不断调整两个距离函数得到的结果:

水平集
假如有一个立体的网格值,可以通过找到网格值中相等的量连成平面,如找到值为0的所有点连成面,就像距离函数那样。
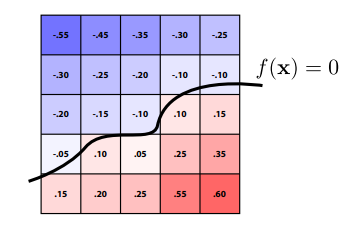
该方法广泛应用于CT,核磁共振等的成像中。






Comments | NOTHING