贝塞尔曲线

贝塞尔曲线是由多个点确定一条曲线，其中，曲线一定经过第一个和最后一个点。

de Casteljau算法

假设有三个点\(b_0\)、\(b_1\)、\(b_2\)。

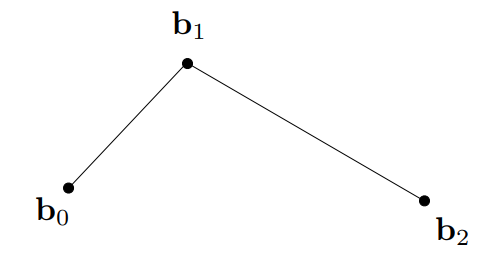
假设一个时间t，取值为\([0,1]\)。在时间t时，在线段\(b_0 b_1\)上取一点\(b_0^1\)，使得\(b_0 b_0^1:b_0^1 b_1=t:(1-t)\)

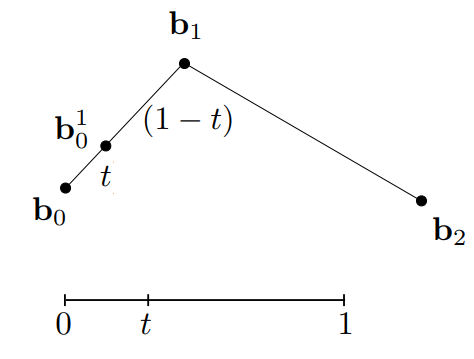
同时，在线段\(b_1 b_2\)上做同样的操作，找到一点\(b_1^1\)，使得\(b_1 b_1^1:b_1^1 b_2=t:(1-t)\)

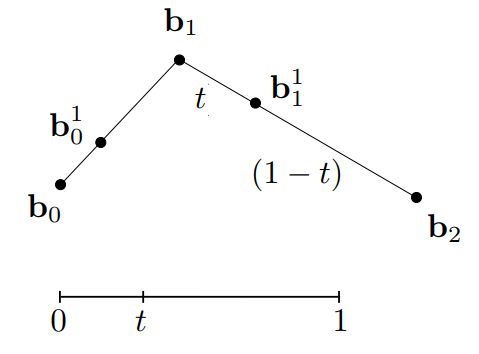
然后再将\(b_0^1 b_1^1\)连起来，并在\(b_0^1 b_1^1\)上找到一点\(b_0^2\)，使得\(b_0^1 b_0^2:b_0^2 b_1^1=t:(1-t)\)

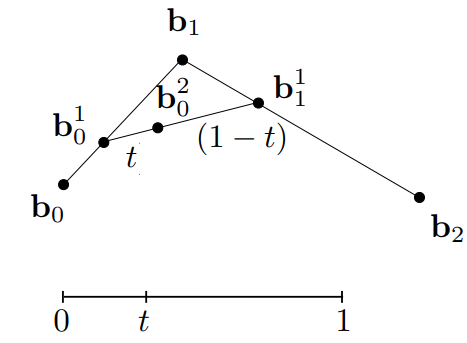
得到的\(b_0^2\)就是所求曲线上的一点。将所有t取值所得到的点连起来，便是所求曲线。

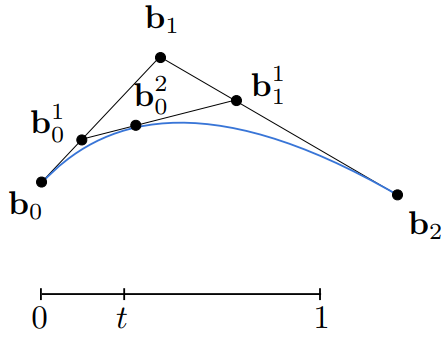
这个曲线是由三个点所决定的，所以叫做二次贝塞尔曲线。

也可以由多个点来决定一条曲线，比如三次贝塞尔曲线：

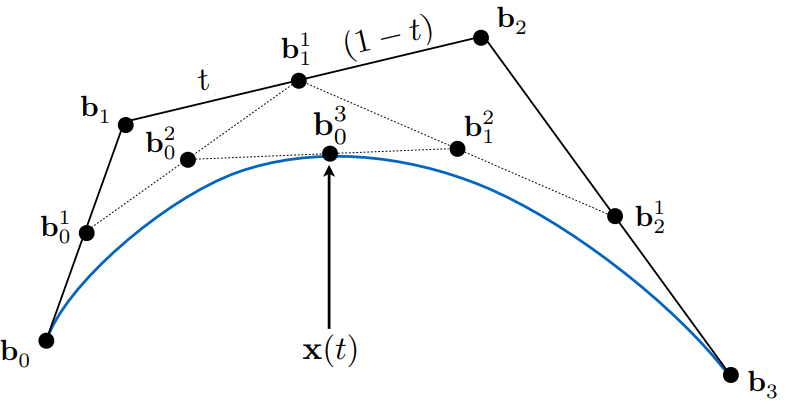
代数公式

de Casteljau算法给出了一个系数金字塔：

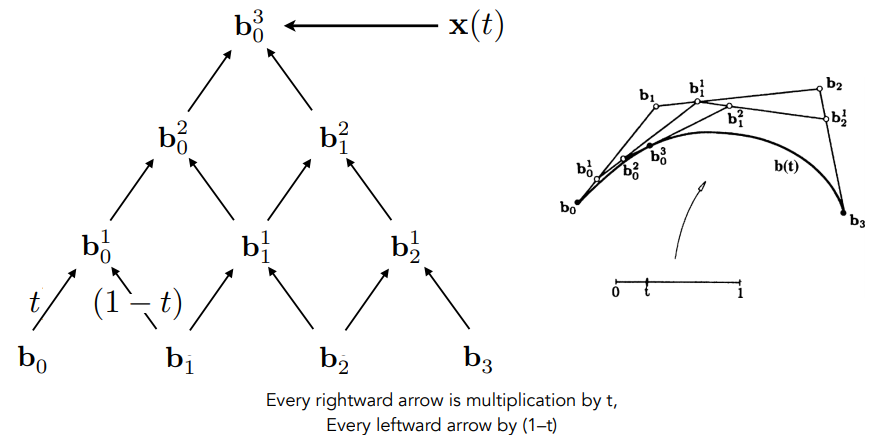
比如二次贝塞尔曲线：

\(b_0^1(t)=(1-t) b_0+t b_1\)
\(b_1^1(t)=(1-t) b_1+t b_2\)
\(b_0^2(t)=(1-t) b_0^1+t b_1^1\)
\(b_0^2(t)=(1-t)^2 b_0+2 t(1-t) b_1+t^2 b_2\)

观察上式可知，b前的系数是对\((t+1-t)^n\)的展开

n阶贝塞尔曲线的伯恩斯坦形式：
\(\mathbf{b}^n(t)=\mathbf{b}0^n(t)=\sum_{j=0}^n \mathbf{b}_j B_j^n(t)\)

\(\mathbf{b}^n\)：贝塞尔曲线阶数n（n次向量多项式）
\(\mathbf{b}_j\)：贝塞尔控制点
\(B_j^n(t)\)：伯恩斯坦多项式

伯恩斯坦多项式：
\(B_i^n(t)=\left(\begin{array}{c} n \ i \end{array}\right) t^i(1-t)^{n-i}\)

该公式不仅能用在二维平面，也可用于三维空间。

性质

贝塞尔曲线的开始和结尾必定经过\(b_0\)和\(b_n\)

其开始和结尾处与初末端线段相切

控制点经过仿射变换后，仍能得到正确贝塞尔曲线

曲线在控制点的凸包内

分段贝塞尔曲线

当控制点变多时，曲线会变得难以控制，微小地改变一个控制点都会影响到整个曲线。
所以每四个控制点为一组，分别计算贝塞尔曲线。
四个控制点中的第一个和最后一个控制曲线的开始和结尾的位置，中间两个控制点控制曲线的形状。

这时会出现问题，在每组连接的位置，曲线会变得不平滑。

发现如果在连接处的两个向量长度相等，方向相等，曲线将在该处变得平滑，即该处的导数也连续。

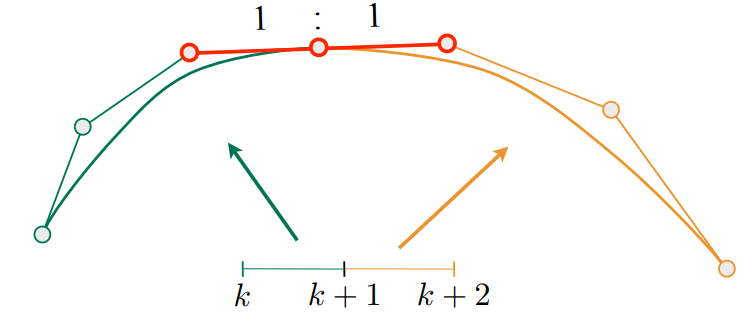
C0连续：在该处连续，即两点相连 \(a_n=b_0\)
C1连续：在该处的一阶导连续 \(a_n=b_0=\frac{1}{2}(a_{n-1} + b_1)\)
C2连续：在该处的二阶导连续
以此类推

曲面

将贝塞尔曲线扩展到曲面，用16个控制点，即4*4个控制点来生成一个曲面。
类似双线性插值，每4个控制点为一组，先计算出t时刻4条贝塞尔曲线的点，再将这4个点作为控制点，再画出一条曲线。
将不同t取值得到的所有曲线连起来，就能得到曲面。