网格细分
Loop细分
Loop细分只能对三角形的模型进行细分
引入新顶点
取每个三角形的每一个边的中点,并相互连接起来。
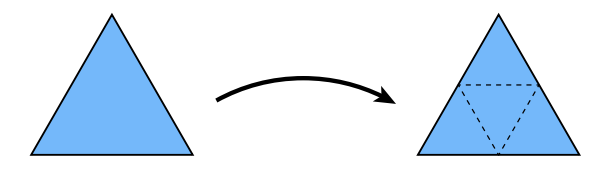
移动顶点
顶点分为新顶点和老顶点:
对于新顶点:新顶点所在边的两个老顶点分别乘\(\frac{3}{8}\),再将该边所在三角形的另外两个顶点分别乘\(\frac{1}{8}\),最后相加,即:\(\frac{3}{8}(A+B)+\frac{1}{8}(C+D)\)
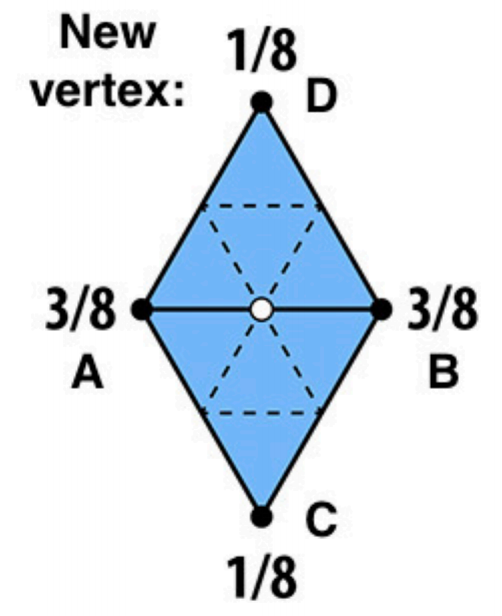
对于老顶点,需要先计算两个值n:顶点度数(顶点所连边的个数),u:如果n=3,\(u=\frac{3}{16}\),否则\(u=\frac{3}{8n}\)。
然后将被修改顶点的值乘\((1-n*u)\),将周围所有的老顶点相加再乘\(u\),最后相加,即:\((1-n*u)*original-position+u*neighbor-position-sum\)
Catmull-Clark细分
Catmull-Clark细分可以对所有的模型进行细分。在该细分中,需要将面分为四边形面和非四边形面。将顶点分为奇异点(顶点度数不等于4)和非奇异点。

引入新顶点
取每个边的中点和每个米面的中点,并连接起来。
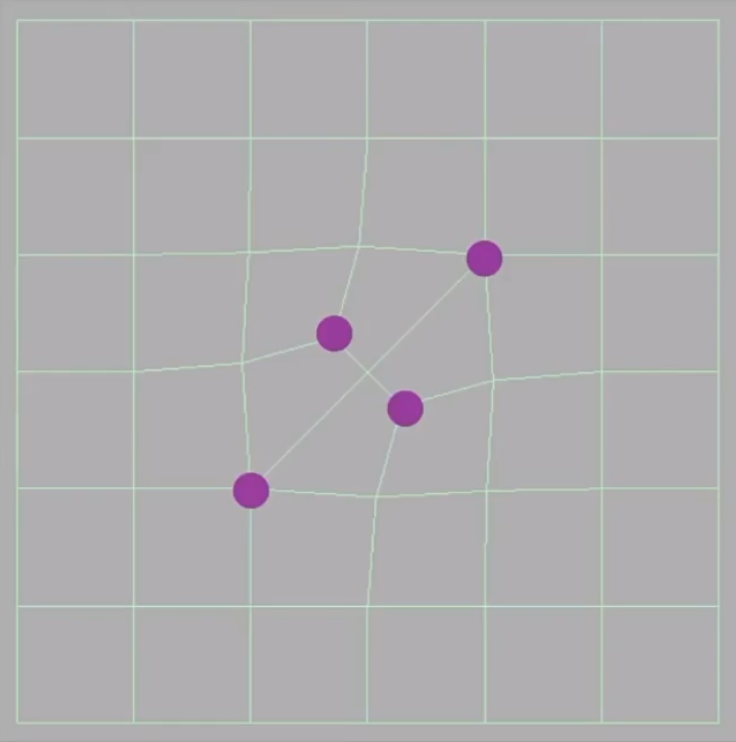
会发现细分时所有的非四边形面都会消失,而奇异点会增加,且每一个非四边形面都会增加一个奇异点。
移动顶点
将顶点分为:老顶点v、在面中间的新顶点f、在边上的新顶点e。
对于在面中间的新顶点:\(f=\frac{v_1+v_2+v_3+v_4}{4}\)
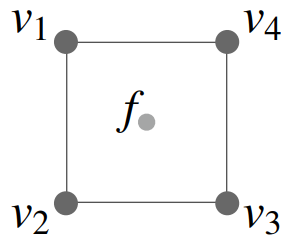
对于在边上的新顶点:\(=\frac{v_1+v_2+f_1+f_2}{4}\)
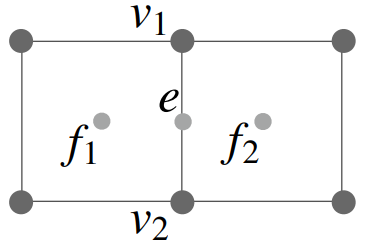
对于老顶点:\(v=\frac{f_1+f_2+f_3+f_4+2(m_1+m_2+m_3+m_4)+4p}{16}\),其中m为边上的点,p为被移动的顶点本身。
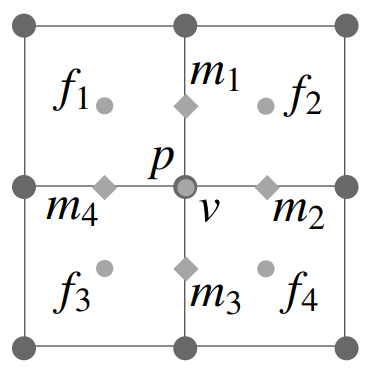
网格简化
⼆次误差度量
它用来表示网格简化带来的误差的大小。
二次误差:新的点应该与它相关联的面的距离的平方和最小。
边坍缩
将一个边的两个顶点进行合并。
假设坍缩每一条边,然后分别计算它们的二次误差。
然后每次选择二次误差最小的边进行坍缩,然后更新被影响的边的二次误差。
可以使用堆或优先队列。
通过局部最优解求取全局最优解,即贪心算法。
阴影映射
从灯光渲染:
将灯光作为相机,从灯光处观察场景,记录下深度图。

从眼睛渲染:
在渲染时计算该点到达灯光的距离,再计算出该点对应在深度图的位置,并得到深度。如果深度大于该点到灯光的距离,则判断该点可以被该灯光直射,否则判断该点无法被灯光直射,即被遮挡。
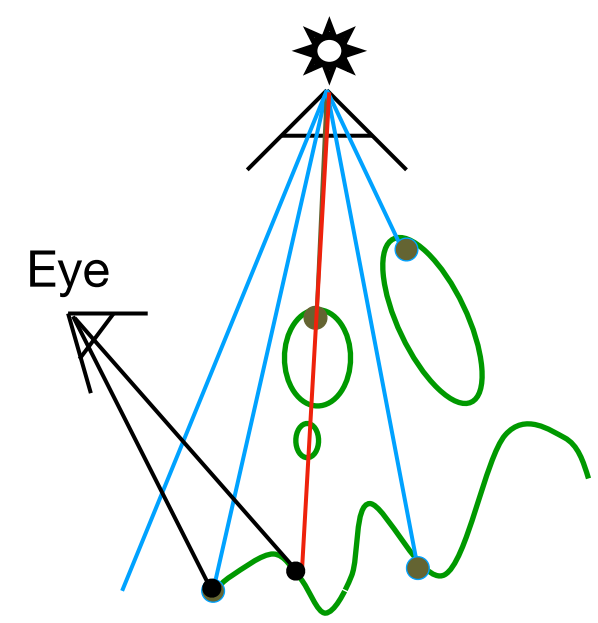

该阴影被称为硬阴影,但在现实中,阴影的的边缘是虚化的,是因为光源并非点光源,是有体积的。
比如说日食现象。
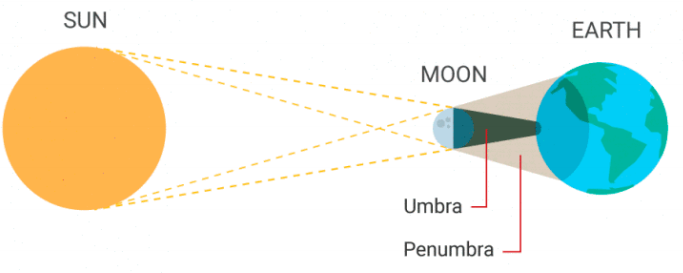






Comments | NOTHING